This tutorial has the purpose of providing detailed information for users of the library.
The tutorial is split into three sections:
- Description of a simple system that will be used for the tutorial;
- Construction of a model for the system;
- Evolution of the model, in terms of simulation and finite/infinite time evolution.
The full code presented in the following is available in C++ as a simple self contained CMake project, or in Python as a script file. The tutorial files are extensively commented. Here on this page instead code snippets are provided for both languages. After following this tutorial, we encourage to play around with the example in order to better understand the behavior of the modeled system.
1 - The system
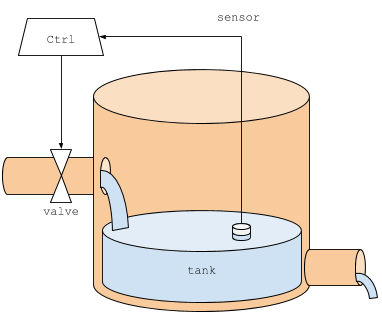
The system described for this tutorial is a watertank system. This example from hydrodynamics revolves around a tank component, which has a controlled input water flow and an output water flow. In particular, the input pressure $p$ is modulated by a valve to obtain the actual input $u$ to the tank. The controller acts in response to a reading $x_s$ of the actual water level $x$. The reading is affected by an uncertainty $\delta$.
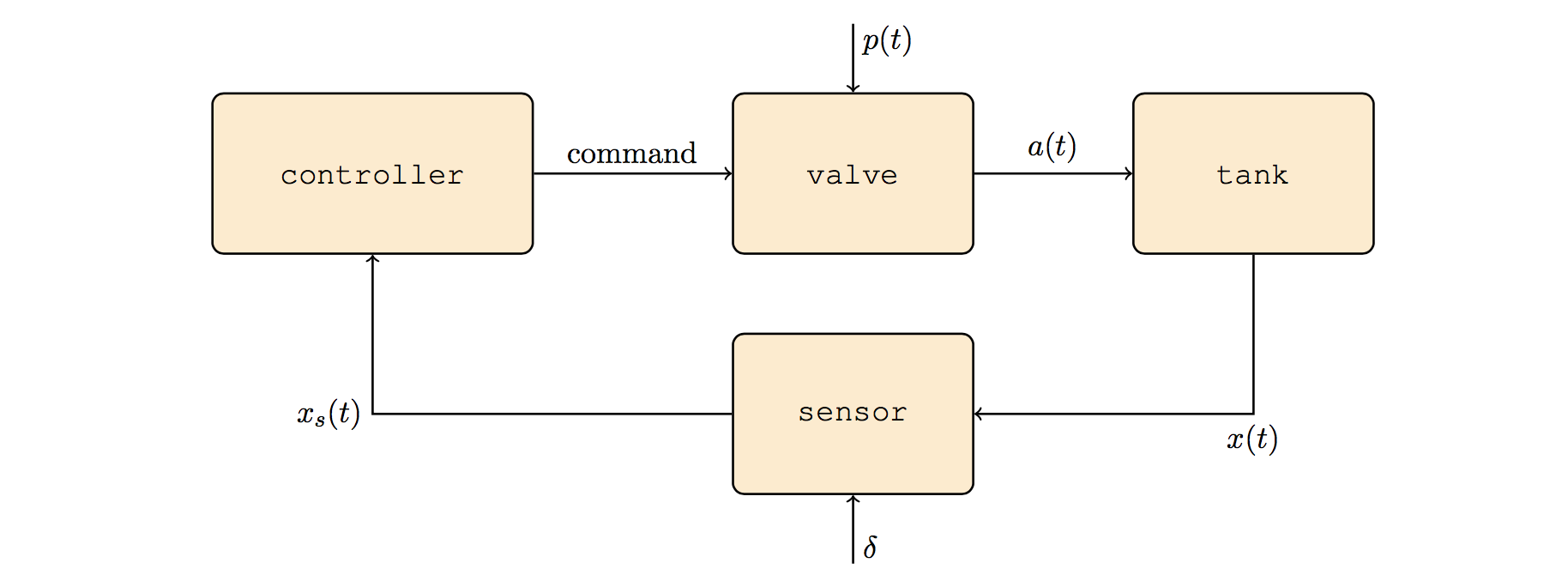
For our system model, we identify three components: the tank, the valve and the controller. In order to provide a model of the sensor, instead, we would need to be able to express the relation $x_s(t) = x(t) + \delta$. This amounts to treating $\delta$ as a noise source. However, Ariadne currently does not yet support noise modeling for hybrid systems, hence we will provide an alternative system model that achieves a similar result.
1.1 - Tank model
The model of the tank is simple, since it involves only one location with no transitions. The dynamics of the water level $x$ is the result of the effect of the input flow $\Phi_i = \beta a$ and output flow $\Phi_o = -\alpha x $, with $\beta = 0.3$ and $\alpha = 0.02$. We are not forced to use a particular name for the location, if only one location is present.
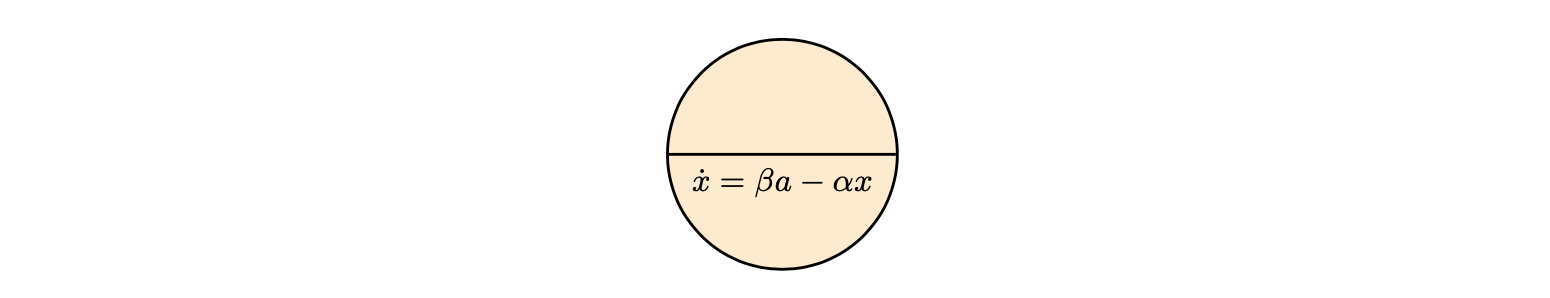
Please note that a more realistic expression for the output flow would require $\Phi_o \propto \sqrt{x}$. However, this choice would have inherent numerical issues around $x = 0$ in the presence of over-approximations, in particular when discretizing the reachable set onto a grid. In order to allow some tweaking of the model parameters in Ariadne without incurring into numerical issues, we preferred to settle for a simplified expression for the tutorial.
1.2 - Valve model
The model of the valve assumes that the valve opens or closes in a finite time $T = 4 s$, with a linear opening or closing. Consequently we define two locations opening and closing in which the dynamics for the aperture $a$ is increasing or decreasing, respectively, with a rate equal to $\frac{1}{T}$. A third and fourth locations opened and closed instead model the valve being fully opened or fully closed, i.e., when $a$ is fixed to a specific value.
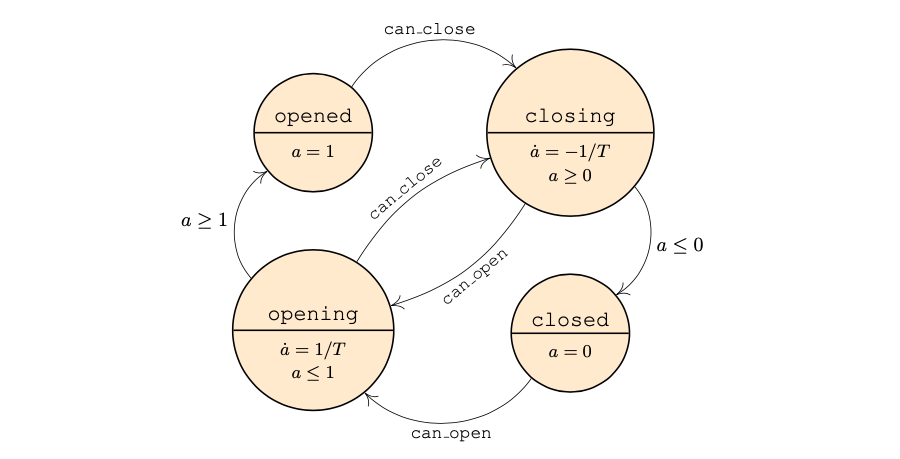
Transitions between locations in this automaton are either internal or external. An internal transition is fired from opening to opened as soon as $a \geq 1$, since $a$ is not allowed to increase further. Similarly, an internal transition is fired from closing to closed as soon as $a \leq 0$, since $a$ is not allowed to decrease further. External transitions have associated event labels, such as can_open and can_close, which synchronise with other automata with the same labels. In this case, since no transition guard is defined, we say that can_open and can_close are input events for the valve automaton: such transitions will be taken when a corresponding output event is fired by another automaton.
It is important to understand that the transitions from opening to closing and vice-versa are necessary to make the model robust to values of the continuous state. While it stands to reason that the closing event will not be fired until the valve has reached the opened location, if the water level is set to a value greater than $h_{\max} - \delta$, then the can_close event will be fired while the valve is still in opening. Subsequently, the valve will switch to opened, but the closing event will not have a corresponding guard for it since the controller will already be in the falling location, for which the closing event is not fireable. The absence of a guard for an event in the composed location implies that the model is ill-defined. The same reasoning goes for the can_open event. These situations may not occur in practice save for the case where the initial set is improperly defined, however a robust model is able to react properly to those situations while a brittle one is bound to raise an error.
Finally, invariants in the opening and closing locations are set as the complements of the guards, in order to model the fact that the transitions are urgent, i.e., if the trajectory reaches a point that satisfies a guard, then it is required to take the transition immediately.
1.3 - Controller model
As discussed previously, the valve is receptive to can_open and can_close commands. The controller is responsible for issuing such commands. In particular, for simplicity we want to have an hysteretic control such that we provide an can_open command when the water level is too low, or a can_close command when the water level is too high.
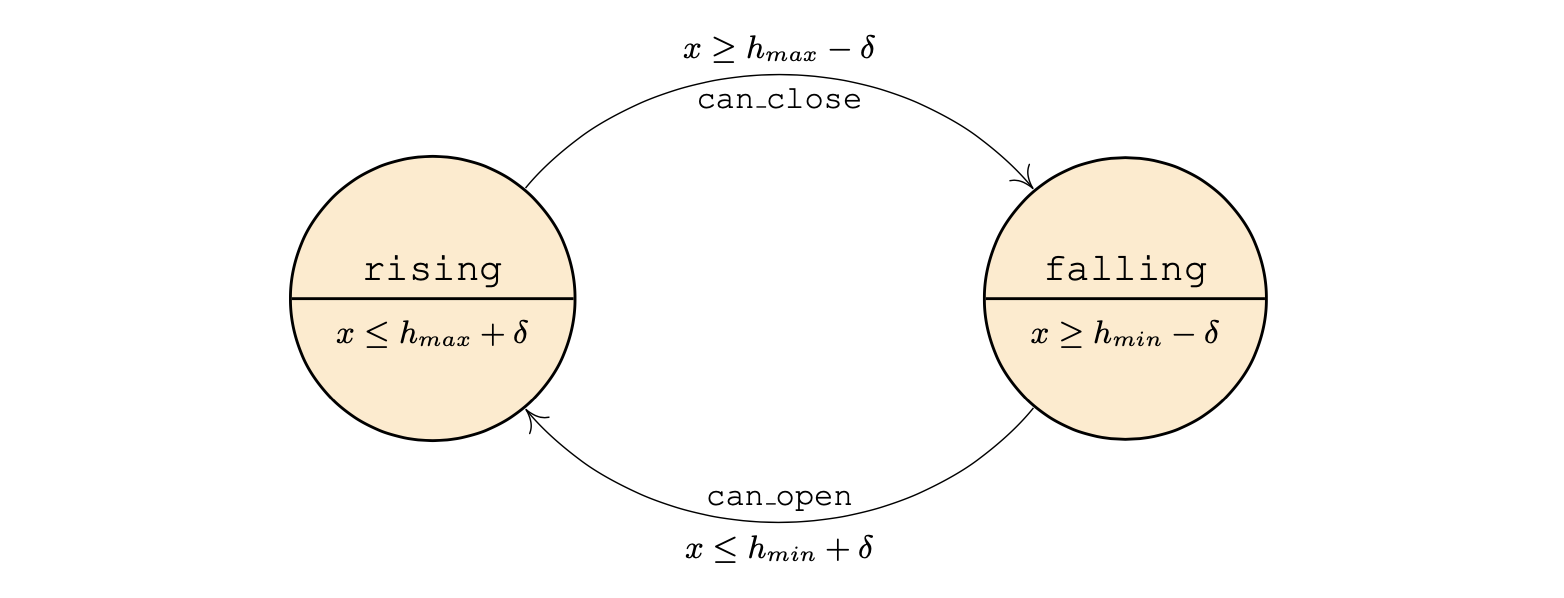
Consequently, the automaton is characterised by two states: rising, when we are operating under the assumption that the water level is rising, and falling, then the assumption is the opposite one. No dynamics are present, instead we provide invariants that establish when transitions must be taken (while guards establish when transitions can be taken).
We define $h_{\max} = 7.75$ meters and $h_{\min} = 5.75$ meters as the acceptable thresholds for the water level. A condition $x \geq h_{\max}$ would trigger the can_close event, while a condition $x \leq h_{\min}$ would trigger the can_open event. However, in our model, we want to provide non-determinism by introducing non-urgent (also called permissive) transitions. This is obtained by enlarging the intersection between a guard and its corresponding invariant: specifically, we enlarge by $2, \delta$, with $\delta = 0.1$ meters. The result of such enlargement is that the transition corresponding to the open event is both taken and not taken for all $x$ values in the $[-\delta+h_{\min},,h_{\min}+\delta]$ interval. Similarly, the close event is both taken and not taken for all $x$ values in the $[-\delta+h_{\max},,h_{\max}+\delta]$ interval.
2 - System model construction
In Ariadne, the construction of a C++ data structure that represents the described model is performed progressively: we start with an empty automaton and we proceed to enrich it with locations, dynamics and transitions.
The costruction of an automaton can be summarised in these steps:
- An automaton object is created;
- Variables, locations and events are declared;
- Dynamics involving variables are added to the automaton;
- Invariants are added, specifying the location;
- Transitions are added, specifying the event, the source and target location, the guard and the reset.
In the following we provide the specific implementation for each of the three components of the tank, valve and controller, followed by a brief discussion on the final composition of the automata. Please note that the details on each operation will not be repeated for all components.
All the code discussed here can be found in the main tutorial file of the repository.
For clarity of presentation, each component is wrapped into its own function that returns the automaton. This approach, while not required, is encouraged in order to maintain large systems, possibly even by using a dedicated header file for each component.
2.1 - Tank
The automaton can be constructed by starting with the following instruction:
HybridAutomaton automaton;
automaton=HybridAutomaton()
This is already a legit automaton, while still empty.
Let us fill it with some behavior. First, we want to define the variables used:
RealVariable aperture("aperture");
RealVariable height("height");
aperture = RealVariable("aperture")
height = RealVariable("height")
Before defining the dynamics for the location, let us introduce some named constants for practical purposes:
RealConstant alpha("alpha",0.02_dec);
RealConstant beta("beta",0.3_dec);
alpha = RealConstant("alpha",dec(0.02))
beta = RealConstant("beta",dec(0.3))
Here we notice how Ariadne requires to specify the type for non-integer literals: a floating point number is simply not accepted since in general it would be rounded to a value that depends on the architecture. It is not necessary to use named constants, since literals are accepted as well.
Then, we add the dynamics with
automaton.new_mode({dot(height)=beta*aperture-alpha*height});
automaton.new_mode([dot(height)<<beta*aperture-alpha*height])
where any nonlinear combination of variables, constants and literals is accepted.
Notice that in this automaton we did not specify the location: while a single location can be introduced, a simplified syntax can be used.
2.2 - Valve
First, we introduce a string variable that will hold the automaton name:
StringVariable valve("valve");
valve = StringVariable("valve")
Then we initialise the valve automaton with
HybridAutomaton automaton(valve.name());
automaton = HybridAutomaton(valve.name())
The motivation for this approach is that we can reuse the string variable to provide sensible labels to the four locations:
DiscreteLocation opening(valve|"opening");
DiscreteLocation closed(valve|"closed");
DiscreteLocation opened(valve|"opened");
DiscreteLocation closing(valve|"closing");
opening = DiscreteLocation({valve:"opening"})
closed = DiscreteLocation({valve:"closed"})
opened = DiscreteLocation({valve:"opened"})
closing = DiscreteLocation({valve:"closing"})
This choice allows to prefix a location name, improving readability. No particular syntax for the location names is necessary. The automaton name is actually independent from the location name prefix and can take on any string value, including being empty as in the case of the tank.
Before adding the corresponding dynamics, we declare constants and variables:
RealConstant T("T",4);
RealVariable aperture("aperture");
T = RealConstant("T",4)
aperture = RealVariable("aperture")
where we notice that constants with integer values can use builtin integers.
Now we can define each mode, i.e. a location for the automaton to which we can attach algebraic/differential dynamics:
automaton.new_mode(opened,{let(aperture)=1});
automaton.new_mode(closed,{let(aperture)=0});
automaton.new_mode(opening,{dot(aperture)=+1/T});
automaton.new_mode(closing,{dot(aperture)=-1/T});
automaton.new_mode(opened,[let(aperture)<<1])
automaton.new_mode(closed,[let(aperture)<<0])
automaton.new_mode(opening,[dot(aperture)<<+1/T])
automaton.new_mode(closing,[dot(aperture)<<-1/T])
For differential equations we use dot of the variable, while for algebraic equations we use let. The curled parentheses are required since these are lists, in which the equations are separated with commas. In the case of a mix of algebraic and differential equations, each must be defined in its own list; the order of the two lists in new_mode is irrelevant. Finally, modes must be named with the location when multiple locations are present.
Before moving to transitions, let’s declare the events. Note that both invariants and guards must be associated to an event.
DiscreteEvent stop_opening("stop_opening");
DiscreteEvent stop_closing("stop_closing");
DiscreteEvent can_open("can_open");
DiscreteEvent can_close("can_close");
stop_opening = DiscreteEvent("stop_opening")
stop_closing = DiscreteEvent("stop_closing")
can_open = DiscreteEvent("can_open")
can_close = DiscreteEvent("can_close")
Now it is possible to define transitions with the following argument format: source location, event, target location, reset map, guard predicate, event kind.
The event kind is an extra specification required to properly instruct the library on the nature of the transition, essentially by specifying if a transition is urgent or permissive. While being permissive is the conventional semantics for the activation of a transition, by defining a transition as urgent we implicitly define a corresponding complementary invariant with the same event name. This is necessary since checking that the intersection of the guard with the invariant has empty interior (i.e., the condition for urgency) is not possible in the general case. Such is the motivation for an explicit specification of the event kind.
The only fields that are always present in the mode definition are the source/target location and the event label. The reset map must be omitted for a variable controlled by the automaton if the variable equation in the target location is algebraic (since it is already defined). Note that in all the other cases a reset must always be defined, even if it’s the identity: this is due to the fact that in general more than one automaton may control the variable (each one on separate locations), therefore we can’t assume to default to the identity map for a given automaton. The guard and event kind need to be omitted instead if the event is an input event, since those are defined in another automaton.
automaton.new_transition(closed,can_open,opening,{next(aperture)=aperture});
automaton.new_transition(opening,stop_opening,opened,aperture>=1,EventKind::URGENT);
automaton.new_transition(opened,can_close,closing,{next(aperture)=aperture});
automaton.new_transition(closing,stop_closing,closed,aperture<=0,EventKind::URGENT);
automaton.new_transition(closed,can_open,opening,[next(aperture)<<aperture])
automaton.new_transition(opening,stop_opening,opened,aperture>=1,URGENT)
automaton.new_transition(opened,can_close,closing,[next(aperture)<<aperture])
automaton.new_transition(closing,stop_closing,closed,aperture<=0,URGENT)
2.3 - Controller
The construction of the controller for the system involves the usual constants and variable declarations:
RealConstant hmin("hmin",5.75_dec);
RealConstant hmax("hmax",7.75_dec);
RealConstant delta("delta",0.02_dec);
RealVariable height("height");
StringVariable controller("controller");
hmin = RealConstant("hmin",dec(5.75))
hmax = RealConstant("hmax",dec(7.75))
delta = RealConstant("delta",dec(0.02))
height = RealVariable("height")
controller = StringVariable("controller")
and the automaton construction:
HybridAutomaton automaton(controller.name());
automaton = HybridAutomaton(controller.name())
after which we can introduce the events:
DiscreteEvent can_open("can_open");
DiscreteEvent can_close("can_close");
DiscreteEvent must_open("must_open");
DiscreteEvent must_close("must_close");
can_open = DiscreteEvent("can_open")
can_close = DiscreteEvent("can_close")
must_open = DiscreteEvent("must_open")
must_close = DiscreteEvent("must_close")
In opposition to the tank automaton, the controller “reads” the height variable; similarly, it “writes” the can_open and can_close events. The must_open and must_close events will be associated to invariants in order to define the $2\delta$ range of nondeterminism when starting the opening/closing of the valve.
The two locations are defined in the usual way:
DiscreteLocation rising(controller|"rising");
DiscreteLocation falling(controller|"falling");
rising = DiscreteLocation({controller:"rising"})
falling = DiscreteLocation({controller:"falling"})
and the modes are created without dynamics, since the controller has none:
automaton.new_mode(rising);
automaton.new_mode(falling);
automaton.new_mode(rising)
automaton.new_mode(falling)
Then we associate invariants to modes with:
automaton.new_invariant(falling,height>=hmin-delta,must_open);
automaton.new_invariant(rising,height<=hmax+delta,must_close);
automaton.new_invariant(falling,height>=hmin-delta,must_open)
automaton.new_invariant(rising,height<=hmax+delta,must_close)
where we see that we need to provide the location, the predicate and an event.
Moving to transitions, we have the following:
automaton.new_transition(falling,can_open,rising,height<=hmin+delta,EventKind::PERMISSIVE);
automaton.new_transition(rising,can_close,falling,height>=hmax-delta,EventKind::PERMISSIVE);
automaton.new_transition(falling,can_open,rising,height<=hmin+delta,PERMISSIVE)
automaton.new_transition(rising,can_close,falling,height>=hmax-delta,PERMISSIVE)
that are specified as permissive and no reset is involved since the automaton controls no variable. After composition, these transitions will supply the guard and event kind for the same event in the transitions of the valve automaton.
Finally, we note how we necessarily omit the reset when no internal or output variable is present.
2.4 - Composition
The Ariadne library currently supports only horizontal composition, meaning that two or more automata at the same level of abstraction can be composed to form a more complex automaton. Ariadne does not yet support vertical modularity in terms of different levels of abstraction and encapsulation. Consequently, we assume that all the automata are represented on a common “horizontal namespace” where all variable and event labels are shared.
In order to create the composed automaton, it is as simple as this:
CompositeHybridAutomaton system("watertank",{get_tank(),get_valve(),get_controller()});
system = CompositeHybridAutomaton("watertank",[get_tank(),get_valve(),get_controller()])
which creates an object that complies to the same interface as a hybrid automaton but internally holds the list of the components.
It is possible to provide a system name as a first argument, again followed by the list of the automata.
For efficiency purposes, actual composition is made dynamically during evolution, meaning that consistency of each location of the composition cannot be checked before evolution.
3 - System model evolution
In this section we provide information on how to analyse a system, in terms of finite time simulation, finite time rigorous evolution, finite time rigorous evolution using a grid and infinite time rigorous evolution.
The first step is the preparation of a C++/Python executable. Let us examine the C++/Python files from the top. To work with the Ariadne library it is necessary to start by including the top header for user consumption (C++) or to import the pyariadne module (Python):
#include <ariadne.hpp>
from pyariadne import *
The content of the main function revolves around these steps:
- Collect command-line input;
- Compose the system to analyse;
- Print the system;
- Simulate the system;
- Construct an evolver;
- Evolve the system;
- Construct a reachability analyser;
- Compute reachability.
Command-line input can be supplied to the tutorial file using several arguments. If running the file with the -h argument you obtain a list of the arguments supported, where the default values are shown. The code to add acquisition of command line interface arguments is
if (not CommandLineInterface::instance().acquire(argc,argv)) return -1;
from sys import argv
if not CommandLineInterface.instance().acquire(argv): exit()
You might be particularly interested in increasing the value of the verbosity, to obtain more information along evolution. If you need colored syntax highlighting for logging, choose a theme.
In the following we detail the implementation for the three evolutions. For a better understanding of the required code, each evolution routine in the tutorial file contains all the necessary variables and calls. However, the code will be commented below only once, hence we suggest to follow the tutorial in order.
3.1 - Finite time simulation
Within the simulate_evolution function we provide the code for simulating the system, i.e., returning a single trajectory obtained by joining evolution points obtained via approximation.
The integrator used to evolve the system in the continuous space relies on the classic Runge-Kutta method.
First, we instantiate the simulator:
HybridSimulator simulator;
simulator.set_step_size(0.01);
simulator = HybridSimulator()
simulator.set_step_size(0.01)
which can only take a step size. For numerical settings in general we accept double-precision values, since an undefined rounding of these values does not affect the correctness of the result (while the value of a constant affects the behavior of a system instead). That’s all for the configuration of a simulator object, which is very simple.
Then we define the initial point for simulation:
HybridRealPoint initial_point({valve|opened,controller|rising},{height=7});
initial_point = HybridRealPoint(DiscreteLocation({valve:opened,controller:rising}),{height:Real(7)})
in which we assume, similarly to automaton definition, that the variables and string constants required have been declared earlier in the function. Here we see that we define the location for a composite system by creating a list of location names, where the order is irrelevant. This location is paired with a real point, which is given by another list of values for each differential variable (therefore the aperture is not supplied, since it is algebraic in the given location).
Along with the initial point, we must define the termination criterion:
HybridTerminationCriterion termination(30.0_x,5);
termination = HybridTerminationCriterion(Real(exact(30.0)),5)
A hybrid termination criterion can involve three criteria: a maximum continuous time, a maximum discrete time (i.e., number of transitions), and a set of discrete events. The semantics is such that as soon as one criterion is hit, evolution stops. In particular, for the discrete events, evolution stops as soon as a transition associated with one of the provided events is triggered. In our specific case we want to enforce termination after either 30 seconds or 5 transitions.
Now we can run the simulation, returning an orbit object containing the list of points for each location, along with their simulation times:
auto orbit = simulator.orbit(system,initial_point,termination);
orbit = simulator.orbit(system,initial_point,termination)
If we used a sufficiently high verbosity in C++, the output would be a series of lines similar to the following:
t=23.149999 #e=2 p=[5.782] l=(controller|falling,valve|closed) e=[can_close,stop_closing]
in which we display the current time, the number of events triggered, the point in the differential variables only, the location and the trace of the events in order of triggering.
Finally, we can plot the orbit on different projections:
plot("simulation_t-height",Axes2d(0<=TimeVariable()<=30,5<=height<=9),orbit);
plot("simulation_t-aperture",Axes2d(0<=TimeVariable()<=30,-0.1<=aperture<=1.1),orbit);
plot("simulation_height-aperture",Axes2d(5<=height<=9,-0.1<=aperture<=1.1),orbit);
plot("simulation_t-height",Axes2d(0,TimeVariable(),30,5,height,9),orbit)
plot("simulation_t-aperture",Axes2d(0,TimeVariable(),30, -0.1,aperture,1.1),orbit)
plot("simulation_height-aperture",Axes2d(5,height,9, -0.1,aperture,1.1),orbit)
Consequently, we need to supply a file name, an Axes2d object that specifies the range of the variables (with the special TimeVariable() variable if we want to refer to time) and the set to be plotted. Each file will be a png figure with the trajectory constructed by joining the points.
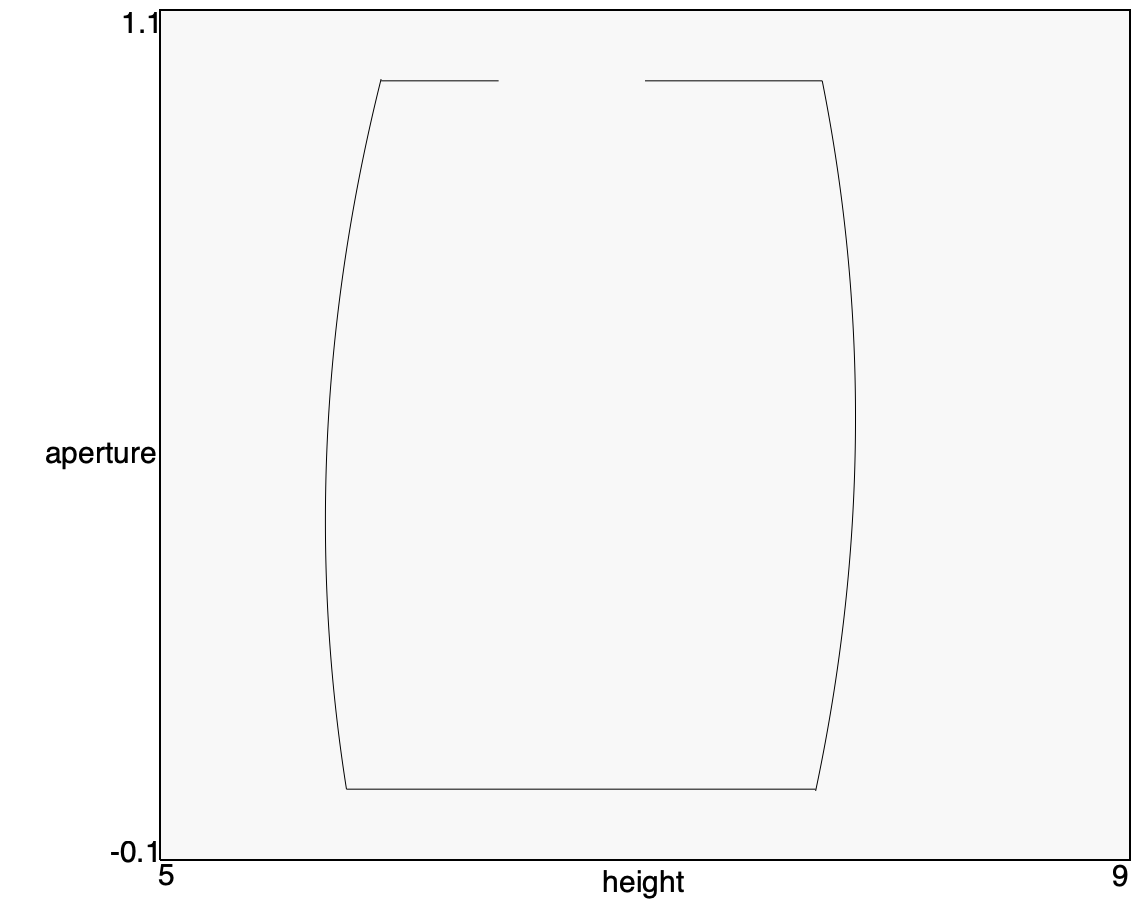
The figure above shows the trajectory, starting from the top and moving clockwise: the height increases until the condition for closing the valve is triggered. The value closes gradually, hence the height still increases slightly before decreasing. When the aperture is zero, the height continues dropping until the condition for opening the valve is triggered. Again, since the opening is gradual, the height drops a bit before increasing again. At a fully opened valve, the height continues increasing until hitting the time limit of 30 seconds according to the termination criterion.
3.2 - Finite time rigorous evolution
The first step is the creation of a GeneralHybridEvolver object, which provides methods for finite time evolution. Since this is slightly more complicated than a simulator, we wrapped it into a create_evolver function for this tutorial.
First, we create the evolver from the system:
GeneralHybridEvolver evolver(system);
evolver = GeneralHybridEvolver(system)
then we configure the evolver:
evolver.configuration().set_maximum_enclosure_radius(3.0);
evolver.configuration().set_maximum_step_size(0.25);
evolver.configuration().set_maximum_enclosure_radius(3.0)
evolver.configuration().set_maximum_step_size(0.25)
Here the most important setting is called a maximum step size since in general the integration step must be small enough to allow the identification of a bounding box for the flow set. If the provided value does not guarantee such condition, the library internally reduces the provided value until the value is acceptable. However, if the step size is reasonably small with respect to the dynamics, it is usually the case that a bounding box is identified with no halving.
Another relevant setting is the maximum enclosure radius, used to decide if an enclosure is too large: if this is the case, then the evolution stops prematurely.
By printing the configuration with
ARIADNE_LOG_PRINTLN("Evolver configuration: " << evolver.configuration());
print("Evolver configuration:",evolver.configuration())
we see other settings which we will not comment here but that are documented in the source code.
As soon as the evolver is set up, we can perform finite-time evolution by computing the orbit of the automaton in a way quite similar to the simulator. The notable differences here are two-fold:
- The initial set accepts intervals for variables;
- The semantics (i.e., upper/lower) must be specified.
Let’s show how to achieve the former:
HybridBoundedConstraintSet initial_set({valve|opened,controller|rising},{6.9_dec<=height<=7});
initial_set = HybridBoundedConstraintSet({valve:opened,controller:rising},[(dec(6.9)<=height)<=7])
The initial set is a HybridBoundedConstraintSet instead of a HybridRealPoint and it accepts interval values. If a singleton value is preferred, the syntax {height==7} needs to be used instead (note that we used {height=7} for a point).
Semantics goes directly in the evolution call:
auto orbit = evolver.orbit(initial_set,termination,Semantics::UPPER);
orbit = evolver.orbit(initial_set,termination,Semantics.UPPER)
Ariadne uses two semantics: upper and lower. Such difference essentially amounts to deciding whether a transition should be taken in the presence of approximations. Since Ariadne operates on over-approximated sets, if such a set partially crosses a guard, then it is not always decidable whether the exact set either completely crosses, partially crosses or does not cross at all. If that is the case, we want to provide two semantics of evolution: allow or disallow a spurious transition. In the first case of upper semantics we end up with an approximate reachable set which is a (possibly) unbounded over-approximation of the exact reachable set; in the second case of lower semantics instead we have a bounded over-approximation, where the bound is essentially the diameter of the flow tube. However, under lower semantics we may terminate evolution earlier, hence the over-approximation may be of a subset of the reachable set. In addition, lower semantics disallows subdivisions of a set, since in that case one of the two splits may not contain any point of the exact reachable set; if such split set then diverges in respect to the other split set, the bound on the over-approximation increases in an uncontrolled way.
If we used a sufficiently high verbosity, we would see a series of log outputs such as:
#w=2 #r=1332 #f=44 #e=2 #p=2 #c=2 t=[23.034064,23.250000] dwt=[14.250000,14.250000] c=[5.772] r=0.044247515 te=0. se=0.0000173 l=(controller|falling,valve|closed) e=[can_close,stop_closing]
There are several extra fields here compared to the simulator; let’s introduce the most important ones. First, #w represents the number of working sets, i.e., trajectories currently being processed. Since there is nondeterminism due to the permissive transitions, this produces a bundle of trajectories which need to be processed separately. Also, since we are dealing with sets rather than points, the time itself is an interval, here under the t field, and the set itself is summarised by a center c and a radius r. The number of reachable sets currently processed is given by #r instead.
Finally, plotting the orbit is exactly the same as in the case of simulation, where only the file names are changed.
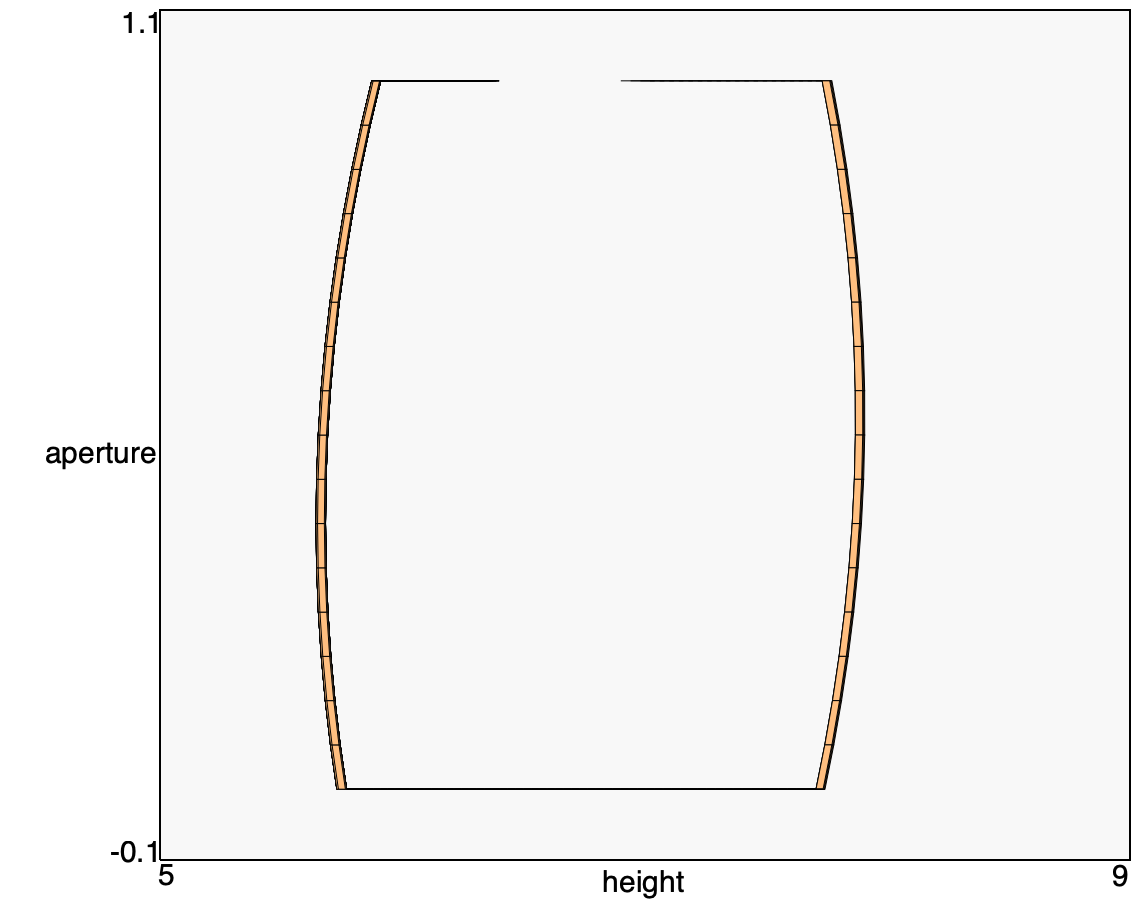
Comparing the figure above with the corresponding one from the simulator we see how the evolver is able to consider the permissive transitions associated with the start_closing and start_opening events. The bundle of trajectories contracts into one line after the valve is fully closed or opened, though it must be specified that all the overlapping reachable sets still need to be computed and plotted.
3.3 - Finite time rigorous evolution using a grid
In this subsection we show the result of performing upper reach rigorous evolution. The output of this routine is the set of points reached by the system if evolved for finite time, while relying on periodic discretisations of the reached set. To do this we rely on a reachability analyser, which differs from an evolver for the use of a grid. A grid is a partitioning of the state space such that difference/subtraction operations can be performed effectively. Reachable sets in the analyser are therefore periodically discretised by overapproximation onto cells in the grid, forming a grid paving.
Using discretisations we are able to perform more scalable evolution in the presence of multiple trajectories coming from non-determinism or, in general, large evolution sets: we can arbitrarily split those sets, while the paving prevents an inefficient superposition of trajectories.
As with the evolver, we provided a function in the tutorial dedicated to the construction of the evolver. An analyser requires an underlying evolver:
HybridReachabilityAnalyser analyser(evolver);
analyser = HybridReachabilityAnalyser(evolver)
After the instantiation we can configure the analyser:
analyser.configuration().set_maximum_grid_fineness(6);
analyser.configuration().set_lock_to_grid_time(5);
analyser.configuration().set_maximum_grid_fineness(6)
analyser.configuration().set_lock_to_grid_time(5)
in which the most important setting is the maximum grid depth, a (small) integer that determines the number of times that we can subdivide a given base cell of the grid; the higher the value, the more accurate the discretisation, but also the larger the number of cells and consequently the more computationally demanding the evolution. The lock to grid time instead determines the period (in seconds) between discretisations onto the grid. A small value allows to promptly identify the end of infinite time evolution, but it also causes more frequent overapproximations.
As with the evolver, we can print the configuration:
ARIADNE_LOG_PRINTLN("Analyser configuration: " << analyser.configuration());
print("Analyser configuration:",analyser.configuration())
The final time is now defined as a hybrid time, but with the same arguments as before:
HybridTime final_time(30.0_dec,5);
final_time = HybridTime(dec(30.0),5)
In order to run the upper reachability routine, we set up the same initial set as for the evolver, implicitly using upper semantics:
auto upper_reach = analyser.upper_reach(initial_set,final_time);
upper_reach = analyser.upper_reach(initial_set,final_time)
Plotting again follows the same syntax as for the previous evolutions:
plot("upper_reach",Axes2d(5<=height<=9,-0.1<=aperture<=1.1),upper_reach);
plot("upper_reach",Axes2d(5,height,9,-0.1,aperture,1.1),upper_reach)
but we must note that for grid sets timing information is discarded, therefore we can’t plot versus time.
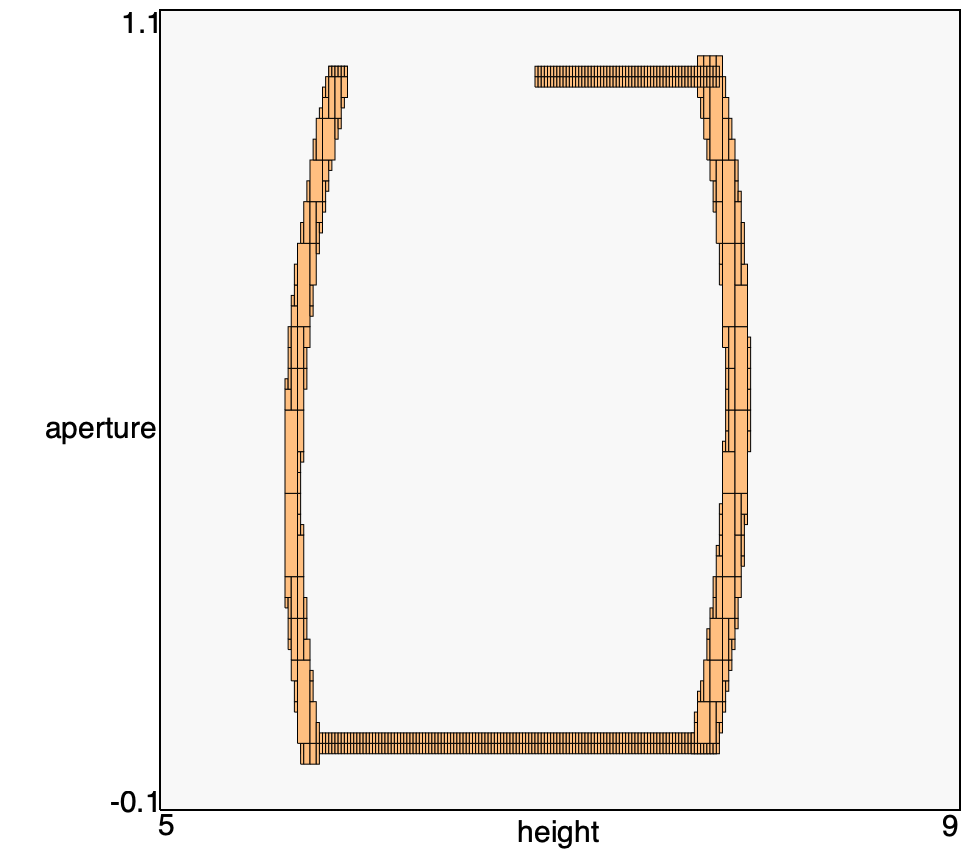
In the figure above we see the corresponding finite time evolution when using a grid. Since the grid is tuned for each location, we notice that the cells have different sizes in different regions. In particular we note that the section of the trajectory where the valve is opened/closed is made of two cells. This is due to the alignment of the grid, which can be configured, though in general is difficult to choose a priori in an effective way. We also note how adjacent cells can be joined into larger cells. As the maximum grid depth increases, the edges of the reachable set become less jagged and the radius generally improves.
Finally, it is apparent that evolution stops earlier, as soon as the fifth location is hit. This is a result of the loss of timing information due to the use of grid sets.
3.4 - Infinite time rigorous evolution
In this subsection we show the result of performing outer chain reach rigorous evolution. The output of this routine is the set of points reached by the system if evolved for infinite time. In order to achieve this in a finite execution time, we again rely on a reachability analyser, in order to allow the required difference/subtraction operations in an efficient and effective way.
Compared to the upper reach case, an important additional configuration setting is the bounding domain that enforces termination if reached. The motivation is that the infinite time reachable set may be unlimited, either intrinsically to the system or numerically due to large overapproximations that prevent convergence. The bounding domain allows to avoid the explosion of the number of cells reached, which would ultimately deplete the available memory.
In order to run the outer chain reachability routine, we set up the same initial set as for the evolver, while the semantics is implicitly the upper one, since we must guarantee to return all reachable points:
auto outer_chain_reach = analyser.outer_chain_reach(initial_set);
outer_chain_reach = analyser.outer_chain_reach(initial_set)
Plotting again follows the same syntax as for the previous evolutions:
plot("outer_chain_reach",Axes2d(5<=height<=9,-0.1<=aperture<=1.1),outer_chain_reach);
plot("outer_chain_reach",Axes2d(5,height,9,-0.1,aperture,1.1),outer_chain_reach)
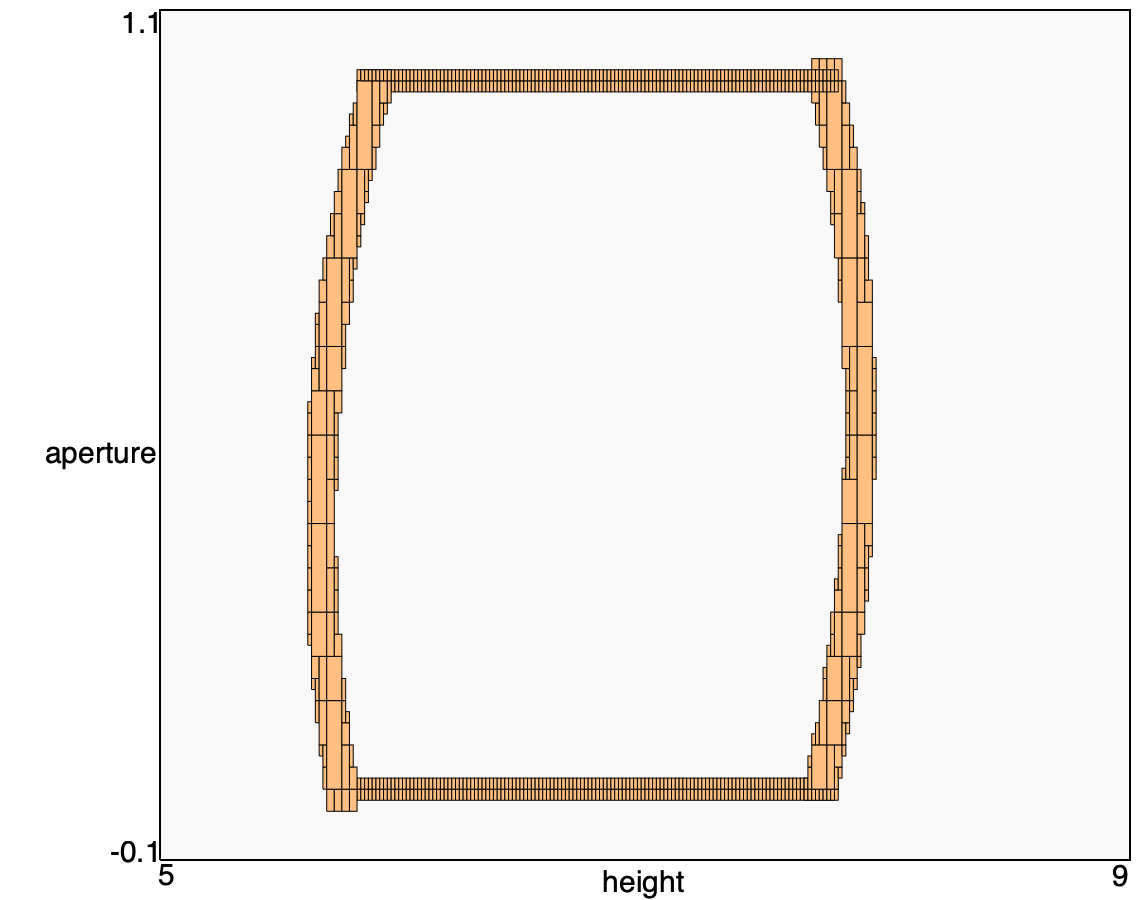
In the figure above we see the outer chain reachable set. Compared with upper reach, first we see that the whole evolution is performed. For infinite time reachability, the automaton usually needs to perform several “rounds” of the hysteretic cycle. This introduces extra cells, apparent in the left side of the figure. If the lock to grid time if increased, the average radius on one run is improved, but this does not guarantee an overall smaller number of cells and a faster convergence. The settings values that allow convergence in a finite and small number of rounds are not trivial to find and require some trial and error.
4 - What’s next
This tutorial is meant to be as compact as possible, by giving a glimpse of the capabilities of the library. We suggest to play a bit with the configuration settings, in order to see the impact on the plotted results. Then it will also be interesting to increase the initial set, which would make evolution more demanding. Meanwhile, using verbosity values higher than 2 may yield some insight on the inner workings of the library.